The start of the noughties brought a change in fashion with reduced frame sizes, the resurgence in popularity of small rimless and half-rimless mounts and the demise of oversized frames. Some may consider that the dispensing world enjoyed a period of stability benefiting from the relative ease of dispensing smaller lighter frames without any major consideration of lens thickness. But, to coin a phrase, ‘what goes around comes around,’ and now oversized ‘funky’ frames are very much the on trend fashion statement that patients are looking for today.
Against this backdrop it is no wonder that many of us may be rusty when it comes to understanding lens thickness and the considerations required when dispensing lenses.
The following article aims to revisit our understanding of what influences lens thickness, how we can control this and ultimately avoid situations of poor cosmetics and patient dissatisfaction.
Decentration
Today’s standard single vision spectacle lenses are of meniscus form, having a convex spherical front surface and concave back surface. The front surface is referred to as the base and the ultimate power of the lens is the sum of the front and back curves combined with the influence of the thickness.
Positive lenses are always thicker in the middle than at the edges and negative lenses thicker at the edges. This thickness is dictated by the power and blank size.
In order to minimise lens thickness, the smallest possible blank should be used and this is possible when the frame PD (boxed centre distances) exactly matches the patient’s PD as no decentration of the lens will be required. As a rule of thumb, when dealing with medium to high prescriptions, 3mm decentration per eye should be considered as a maximum in order to maintain cosmetic acceptability. However, consideration of the patient’s existing spectacles may also prove useful as a guide.
If we consider a frame with boxed centre distances of (52+18) = 70mm and have a patient with a +5.00DS prescription who has a monocular right PD of 32mm and left 27mm, the lenses will need to be decentred 3mm for the right and 8mm for the left (figure 1). If CR39 lenses are used the resultant difference in lens centre thickness is 2.1mm but to the patient the left lens will appear at least twice as thick as the right as much of the lens becomes visible outside the frame.

Figure 1: Asymmetric decentration may cause an unacceptable difference in lens thickness
Frame shape
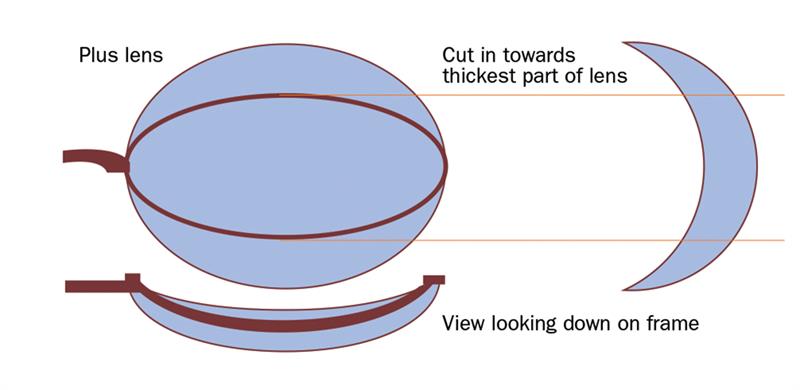
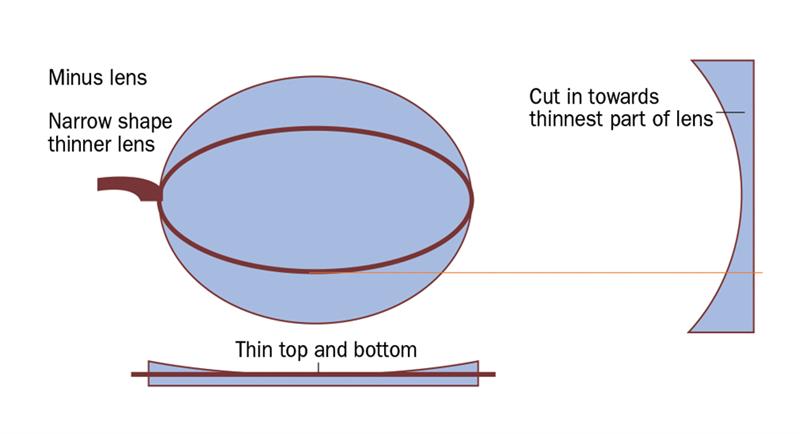
We should remember frame shape plays an important part in the overall appearance of the spectacles, for example even if the utopian ‘zero decentration’ applies, fitting a medium to high plus lens in a frame with a narrow ‘B’ measurement will result in lens thickness top and bottom as we are cutting in to the centre of the lens (figure 2). In contrast, a minus lens is thinner in the centre (figure 3) and so narrow and oval shapes work well.
In the absence of any vertical height specification, most glazing houses will place the vertical lens centres on the horizontal centre line. However, in order to maintain the best possible vision, the optical axis should correspond to the centre of rotation of the eye. With large modern frames, heights should be measured to pupil centres and then dropped 1mm for every 2º of pantoscopic tilt (assuming a vertex distance of 14mm). In doing this we therefore need to consider vertical as well as horizontal decentration.
Inevitably, raising the centre of the spectacles requires larger blanks which not only increases centre thickness on plus lenses but also creates a wedge at the top rim, while negative lenses will have a wedge at the bottom rim. This is not only unsightly but also unbalances the spectacles creating fitting issues.
Incorrect blank size
Often standard stock 65mm lenses in plus powers are used inappropriately, where perhaps 60 / 55 or even 50mm surfaced lenses would be ideal, this will of course result in lenses having no apparent thin edge and both thickness and weight will be increased (figure 4).

The effect of cylinder
Of course, we have not yet considered the effect of cylinder on lens thickness which, depending on orientation and magnitude, can affect the overall appearance of the finished spectacles (figure 5).

If we consider a lens of +4.00DC x 90, the thickest edge of the lens will lie along the plus axis meridian and conversely a lens of -4.00DC x 90 will have its thickest edge at 180 degrees so knowing the cylinder power should allow us to predict exactly where the lens thickness will be. Furthermore, by breaking down a sphero-cylindrical lens in to its cross cylinder form, we can understand where a lens’ thickest and thinnest points will be.
For example, if the following lens were made on a 10 base, applying thin lens theory suggests:
Lens power +4.00 /+4.00 x 180 (figure 6);
+8.00 DC x 180 power meridian, 90 rear curve would be
-2.00 x 90
+4.00D DC x 90 power meridian, 180 rear curve would be
-6.00 x 180
We can see that if the lens is made round, it would have minimum substance at the top and bottom edge (or 90 degree meridian) and its thickest edge at the horizontal (or the 180 degree meridian). However, the thickness of the overall lens can be reduced by employing thickness reduction surfacing techniques (such as Hoya’s METS process). As spectacle frames have an A measurement greater than a B measurement, we can surface the lens down to create an oval or egg-shaped blank as the horizontal thickness offers us no benefit.

The surface reduction techniques that are currently used consider the frame shape and design, optical centration and prescription in order to produce the most cosmetically acceptable results. As a rule of thumb, this process has its greatest impact on positive prescriptions, with positive cylinders of over +1.00DC and axis orientation from 180º to 135º and from 0º through to 45º.
In figure 7 the right and left lenses have the same power and centration but different axis orientation.

The right lens has been surfaced using thickness reduction techniques. The left, however, cannot benefit from this as the axis orientation results in the thinnest edge being at temporal or 180 and surfacing down further would result in the blank becoming too small. In this instance, only using the minimum blank size possible will help.
Let us now consider a negative sphere prescription, for example, if the following lens were made on a 2 base and thin lens theory is applied:
Lens power; -4.00 /+4.00 x 180
-4.00DC x 90 power meridian, 180 rear curve would be
-6.00 x 180
0.00DC x 180 power meridian, 90 rear curve would be
-2.00 x 90
From this we can see that the thickness will be in the horizontal plane at the edge and the lens will be thinnest top and bottom. Figure 8 again shows the risk of different thickness profiles based purely on axis orientation.

Again, if the prescription was -4.00 /+4.00 x 90, then the lens thickness would be at the top and bottom and, given a frame with a narrower B measurement, the thickness will be cut away and differences minimised.
By careful consideration of cylinder power and axis orientation we can evaluate how lens thickness is influenced and guide patients towards the most appropriate lens shapes that are both fashionable and support cosmesis. Table 1 offers a guide to the influence of axis upon cylinder power.

Table 1: Influence of axis upon cylinder power
Base influence
The form of a lens also plays a part influencing lens thickness for any given power. As the front curve is made steeper, a plus lens will become thicker. Flatter forms are slightly thinner, although flattening the lens has the adverse effect of creating oblique astigmatism and therefore reduced image quality and off axis performance. More curved forms often give the impression that the lenses are considerably thicker than their flatter counterparts. This is because the lens appears to bulge out of the frame more and sit further away from the eye, so increasing magnification. By utilising an aspheric front surface, a plus lens can be made thinner, lighter and flatter without the lens performance being compromised. With regard to minus lenses, using lenses with back surface aspherisation will reduce thickness slightly as the rear curve will flatten away from the lens centre.
Increasing refractive index
Often we think of refractive index as one of our key allies in reducing overall lens thickness, and with organic lenses now available in a multitude of indices (ranging from 1.498 right through to 1.76 and, for glass, to 1.9 index) we have a huge choice at our disposal.
With minus prescriptions, switching a patient from a 1.498 index CR39 to a 1.60 index organic lens will, in most cases, reduce edge thickness by at least 1mm as a result of the 1.60 material being made with a lesser centre substance. Add to that the index effect, and the edge thickness on a 65mm -4.00DS sphere reduces by 1.84mm. However, going from 1.60 to 1.67 only reduces thickness by a further 0.41mm.
If we consider a -8.00DS sphere power, moving from 1.60 to 1.67 gives a reduction of 0.89mm and, moving to 1.9 glass, a 2.66mm edge thickness reduction compared to 1.60 index.
Glass has very much fallen out of favour over recent years but, for high myopes, 1.8 and 1.9 index glass lenses offer the most cosmetically appealing results.
Table 2 shows the relationship between index, power and base curve and influence on thickness.
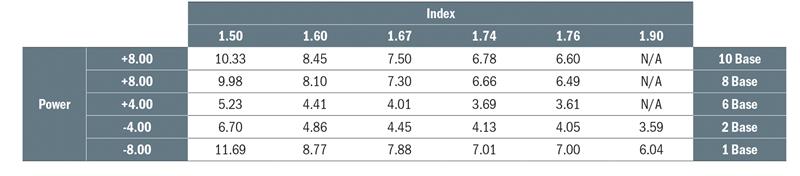
Table 2: Centre thickness (in mm) for plus and edge thickness for minus 65mm lenses made in different index materials (assuming a minimum edge of 0.8mm on plus lenses and minimum centre thickness on minus lenses of 1.2mm – except CR39 where 2.2mm is assumed)
Combining the appropriate use of mid and high index materials with aspheric surfaces can dramatically improve the overall appearance of spectacles, particularly higher plus prescriptions. All lenses can easily be enhanced by the addition of high quality anti-reflection coatings. By reducing unwanted reflections, these coatings can improve minus lenses cosmetically by reducing the appearance of power rings and, for plus lenses, make the lenses appear less bulbous.
Bevel position and rim
While we can minimise and analyse thickness from an overall view point, the crucial outcome is that our patients are happy. As has already been mentioned, the part of the lens showing outside the rim of a frame is how patients perceive the thickness of their lenses. Simply moving up an index, in many cases, results in the patient thinking their lenses are half the thickness. The frame rim thickness and the lens bevel position play an important role in this illusion (see figures 9 and 10).
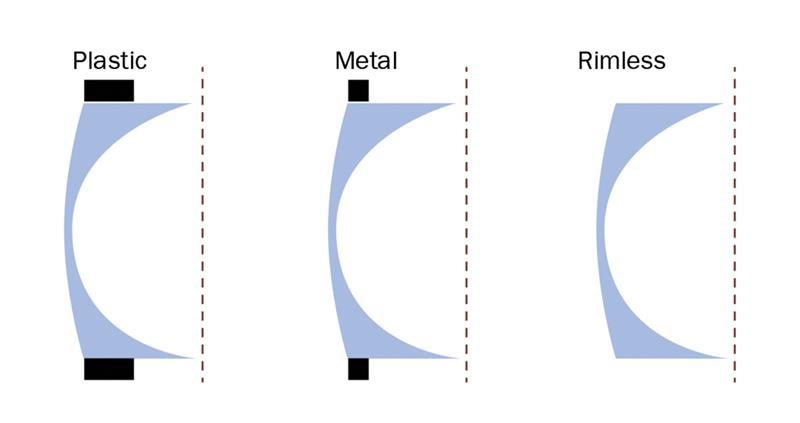
Figure 9: Perceived edge thickness for a positive power lens in different frames
When edging the lenses, care should be taken with all high index organic lenses. For lenses harder than CR39, some older edging machines tend to cut the bevel towards the front surface so that, when fitted into the frame, all the thickness is pushed to the back. Using more modern edging equipment (or controlled bevelling techniques) can place the bevel in a suitable pre-determined location so that some of the lens sits slightly forwards of the front of the frame (or level) so that the majority of the lens remains hidden.
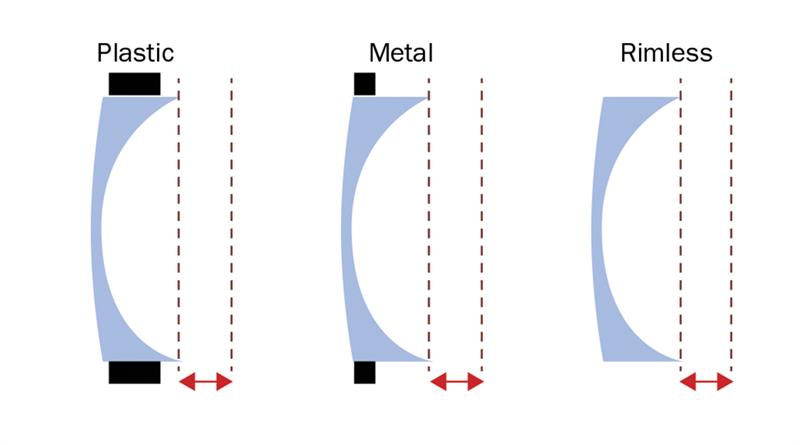
Figure 10: Perceived edge thickness for a negative power lens in different frames (red arrows indicate perceived thickness reduction)
Patients desiring rimless or half-rimless frames should also be made aware that the full lens or part of the lens will be exposed. One of the best ways to do this is to remove a lens from their current spectacles and show them its thickness. Of course, it is sensible to emphasise that this is only a guide to the expected outcome.
The lens in any frame must be of a safe design and have sufficient mechanical strength suitable for the mount. For rimless frames, a minimum thickness at the drill points of 2.2mm is usually required and a 1.8mm edge thickness for half rimless or supra mounts. PNX 1.53 (Trivex), 1.60, 1.67 and some 1.74 materials offer the required properties for these types of frames. However, in plus prescriptions, while these indices may offer flatter lenses, the edge thickness will need to be increased from the usual 0.8mm. This is an extremely important consideration when having plus lenses with positive cylinder axes running in or around 180º, where thickness reduction techniques will be negated by the need to have increased substance for the mount.
Similarly, on low minus prescriptions when smaller frames are used, lenses will need to be surfaced with increased centre substance in order for enough thickness on either side of the groove to avoid chipping or in the case of rimless frames, the required depth for plugs/screws or push fitments to ensure safety.
Prism and prism thinning
On occasion, it may be necessary to incorporate prescribed prism into spectacle lenses in order to aid binocular vision, for example in cases of phoria or tropia. Prism is always prescribed with a base direction, which may be specified as an angle or direction, and this can have a major influence on lens thickness. Plus lenses can be thought of as two prisms with their bases meeting in the middle and a minus lens as two prisms with the apices meeting in the middle of the lens.
If we have a patient with a PD of 60mm and +5.00 DS right and left, dispensing a frame with boxed centre distances of 68mm would require the lenses to be decentred 4mm nasally from each eye in order to place the lens centres directly in front of the pupils. If the same patient was prescribed two dioptres of prism base out each eye this could be achieved by placing the lens centres at 68mm as is indicated by Prentice’s rule as follows;
P = cF therefore in this example 2 = 0.4 x 5 where
P = prism in prism dioptres
c = decentration in cm
F = power of the lens
Of course, if aspherics were to be dispensed achieving prism by decentration is not advisable.
If, however the prism was base in, then the required decentration would be 8mm per eye and the nasal edge would be wedge shaped and very thick. For minus prescriptions, base in prism will help cosmesis as, effectively, the lens centres are moved outwards.
Prism is also used to improve the appearance of progressive lenses by a technique called ‘prism thinning’. A traditional progressive uncut lens has a front curve whose radii reduce as the addition increases, so the top edge is thicker than the bottom. With back surface progressive designs, the rear curve increases in radius as the add increases so again the top of the lens has a greater thickness. By working equal amounts of base down prism into the right and left lenses, the thickness of the progressive lens uncut is equalised. Some manufacturers used base down prism equal to approximately 66% of the addition, however, on short corridor progressives fitted in narrow frames this has the undesirable, adverse effect of creating extra thickness at the bottom of the lens (see figure 11).
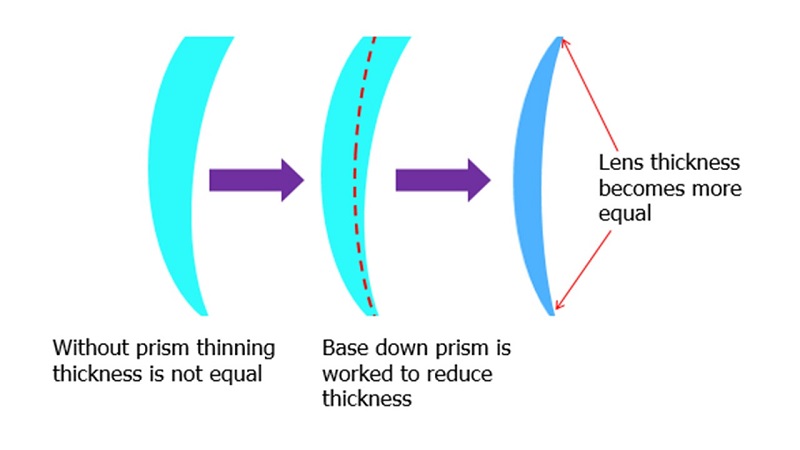
Lens manufacturers are now able to use ‘intelligent prism thinning’ which takes into consideration frame shape, prescription and centration details in order to calculate the very best prism thinning value to even out lens appearance and so make the finished spectacles as aesthetically pleasing as possible. However, more sensitive patients may find the resultant change in image position initially a little strange.
Calculation aids
Calculating lens thickness using the accurate sag formula can be a rewarding exercise and is recommended for a full understanding of the final lens profile. However, there are now many online calculators which quickly give the dispensing practitioner a good idea of likely lens thickness. Most manufacturers now offer ordering systems which accurately scan frames and show a 3D representation of the lenses indicating centre thickness, minimum and maximum edge thickness and its relative position and these are an invaluable tool in modern practice.
Summary
By careful examination of a patients existing spectacles and consideration of prescription cylinder orientation, frame shape, lens material, bevel position, fitting and how these all impact on the physical thickness (along with anti-reflection lens enhancements), we can guide our patients towards the fashionable contemporary styles that suit both their desires and their prescription.
Andy Sanders is a dispensing optician and UK Professional Services Manager for Hoya UK.
Useful reading
- Jalie M. Principles of Ophthalmic lenses. ABDO.
- Meister D, Sheedy JE. Introduction to Ophthalmic Optics. Carl Zeiss Vision Publications.
